| Team Members: | Oluwapelumi Adenikinju1, Julian Gilyard2, Joshua Massey1, and Thomas Stitt3 |
| Graduate Research Assistant: | Jonathan Graf4 Xuan Huang4, and Samuel Khuvis4 |
| Faculty Mentor: | Matthias K. Gobbert4 |
| Client: | Yu Wang1 and Marc Olano1 |
1Department of Computer Science and Electrical Engineering, University of Maryland, Baltimore County,
2Department of Computer Science, Wake Forest University,
3Department of Computer Science and Engineering, Pennsylvania State University
4Department of Mathematics and Statistics, University of Maryland, Baltimore County,

Team 5, from left to right: Joshua Massey, Matthias K. Gobbert, Oluwapelumi Adenikinju, Julian Gilyard, Thomas Stitt, Marc Olano.
About the Team
Our team consists of four undergraduates, Oluwapelumi Adenikinju, Julian Gilyard, Joshua Massey and Thomas Stitt. Oluwapelumi is rising senior in computer engineering at UMBC. Julian is a rising junior in computer science at Wake Forest University. Joshua is a rising sophomore in computer engineering at UMBC. Thomas is a senior in mathematics and computer at Pennsylvania State University.
Problem
In computer graphics, an integral portion of the rendering timeline is solving for the light distribution of a scene. When realism is important, a solution involving global illumination – allowing light rays to bounce before hitting the viewer – is desired. One method that awards particularly good results for diffuse surfaces is the radiosity algorithm, despite the fact that this method is computationally expensive – using it for near-real to real time rendering is not generally practical. Starting with the existing computational radiosity solver rrv, we determine how runtimes can be reduced through a combination of multi-core CPU to massively-parallel GPU architectures available in the cluster maya of the UMBC High Performance Computing Facility .
Computational Methods
Jacobi Method: The original code in rrv solves for the solution of the radiosity equation using a fixed number of iterations in the Jacobi method. This can be physically thought of as one light bounce per iteration, as illustrated visually in the flow chart in Figure 1.
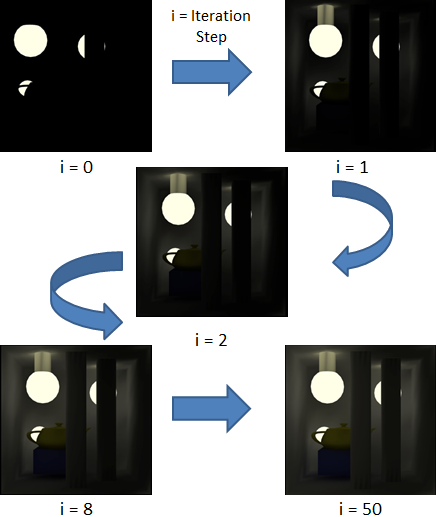
Figure 1: Flow chart of iterations in the Jacobi method.
To provide certainty that the method has actually converged and to save iterations potentially, we reimplement the Jacobi method to compute only until an equilibrium bouncing of light is reached as measured by a tolerance of 10-6 on the relative residual.
BiCG-STAB Method: The Jacobi method can be slow to converge. The BiCG-STAB method is an alternative iterative method, whose convergence speed increases with iterations. It requires twice as much work per iteration, hence might take less time for complex problems that require a large number of iterations with the Jacobi method.
Distributed Computing
CUDA: CUDA is NVIDIA’s library for leveraging the massively parallel architecture of GPUs (graphics processing units). GPUs are designed for SIMD (single instruction multiple data) applications like those used in solving the radiosity equation. CUDA has an efficient package (cuBLAS) for solving linear system, but since the system is composed of vector elements with multiple values (arrays of structures), these methods cannot be used. We implement a dot-product and matrix-vector product for vectors of this type using binary tree reduction and a simple axpby operation for vector scaling and addition.
OpenMP: OpenMP (Open Multi-Processing) is an application programming interface that provides simplified and cross-platform shared-memory parallelization. Memory is considered “shared” when each worker (thread) shares it with all other workers, unless marked worker-private – which is beneficial here since the system matrix of the radiosity equation is large. With OpenMP, portions of serial code are flagged to be run in parallel by work distribution among available threads. We utilize parallelization much like with CUDA to speed up the matrix-vector, dot, and axpby functions.
Results
Runtime results were obtained for four sample scenes of varied patch count and complexity. We see in Table 1 that the scenes used were not complex enough to make apparent the advantages of the reduced number of iterations of BiCG-STAB method, due to its increased cost per iteration.
| Jacobi | Jacobi | BiCG-STSB | BiCG-STAB | ||
|---|---|---|---|---|---|
| Scene ID | Patch count | iter | runtime | iter | runtime |
| 1 | 1312 | 8 | 0.009 | 3 | 0.010 |
| 2 | 3360 | 28 | 0.045 | 16 | 0.058 |
| 3 | 9680 | 36 | 0.410 | 17 | 0.435 |
| 4 | 17128 | 32 | 0.993 | 17 | 1.157 |
Table 1Parallelization on the other hand showed marked improvement with observed run times in units of seconds in Table 2 dropping over an order of magnitude.
| Scene ID | Original | Serial | CUDA | OpenMP |
|---|---|---|---|---|
| 1 | 0.028 | 0.031 | 0.006 | 0.009 |
| 2 | 0.857 | 0.677 | 0.115 | 0.045 |
| 3 | 10.072 | 6.973 | 1.209 | 0.410 |
| 4 | 27.855 | 19.394 | 3.415 | 0.993 |
Table 2
Conclusions
Both computational methods and parallelization were explored with the aim of near-real to real time global illumination solutions to the radiosity algorithm. Given the scenes we tested, OpenMP and CUDA both show substantial runtime improvements while the change from the Jacobi method to the BiCG-STAB method actually resulted in increased runtime due to the method’s complexity. It appears that global illumination problems are not in general best suited for mathematical reformulations, but taking advantage of work distribution seems favorable, no matter the scene complexity.
Links
Oluwapelumi Adenikinju, Julian Gilyard, Joshua Massey, Thomas Stitt, Jonathan Graf, Xuan Huang, Samuel Khuvis, Matthias K. Gobbert, Yu Wang, and Marc Olano. Real Time Global Illumination Solutions to the Radiosity Algorithm using Hybrid CPU/GPU Nodes. Technical Report HPCF-2014-15, UMBC High Performance Computing Facility, University of Maryland, Baltimore County, 2014. Reprint in HPCF publications list
Poster presented at the Summer Undergraduate Research Fest (SURF)
Click here to view Team 1’s project
Click here to view Team 2’s project
Click here to view Team 3’s project
Click here to view Team 4’s project