| Team Members: | Adam Cunningham1, Gerald Payton2, Jack Slettebak1, and Jordi Wolfson-Pou3 |
| Graduate Research Assistant: | Jonathan Graf2, Xuan Huang2, and Samuel Khuvis2 |
| Faculty Mentor: | Matthias K. Gobbert2 |
| Client: | Thomas Salter4 and David J. Mountain4 |
1Department of Computer Science and Electrical Engineering, University of Maryland, Baltimore County,
2Department of Mathematics and Statistics, University of Maryland, Baltimore County,
3Department of Physics, University of California, Santa Cruz,
4Advanced Computing Systems Research Program

Team 4, from left to right: Jack Slettebak, Jordi Wolfson-Pou, Matthias K. Gobbert, Adam Cunningham, Gerald Payton, Thomas Salter.
About the Team
Our team, which consisted of Adam Cunningham, Gerald Payton, Jack Slettebak, and Jordi-Wolfson-Pou, participated in the Interdisciplinary Program in High Performance Computing located in the Department of Mathematics and Statistics at UMBC. Our project was to test the computing capabilities of the maya Cluster using industry benchmarks, a project proposed to us by our clients, Thomas Salter, and David J. Mountain. Assisting us in our research and providing insight and supervision was our faculty mentor, Dr. Matthias K. Gobbert, along with our graduate research assistants, Jonathan Graf, Xuan Huang, and Samuel Khuvis.
Benchmarking
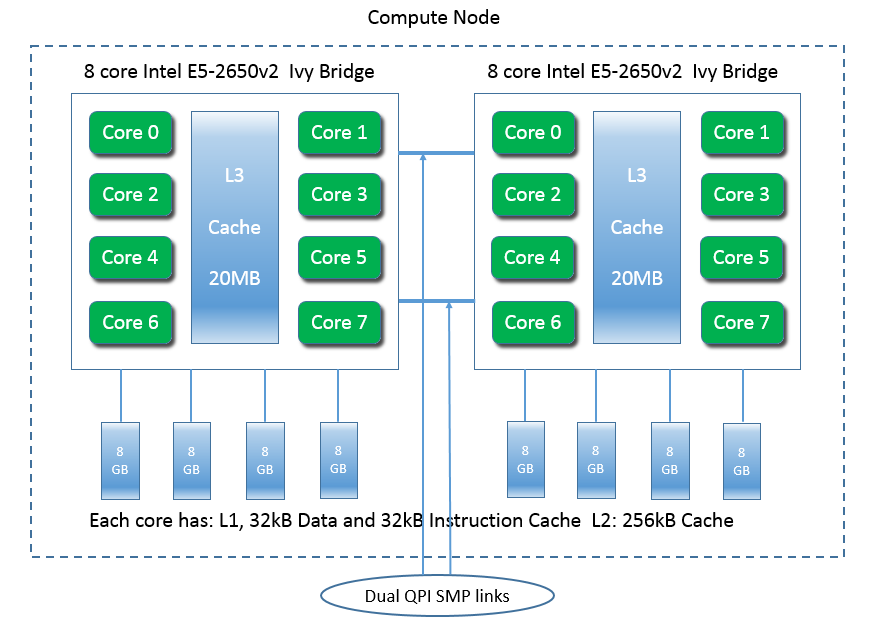
Maya is the 240-node supercomputer in the UMBC High Performance Computing Facility.
The 72 newest nodes have two eight-core Intel E5-2650v2 Ivy Bridge CPUs, with 64 GB memory (in eight 8 GB DIMMs) each, making a single node capable of running 16 processes/threads simultaneously.
The nodes are connected by a high-performance quad-data rate (QDR) InfiniBand interconnect.
The new hardware requires testing and benchmarking to give insight into its full potential. We report here on the High Performance Conjugate Gradient (HPCG) Benchmark developed by Sandia National Laboratories.
HPCG Benchmark
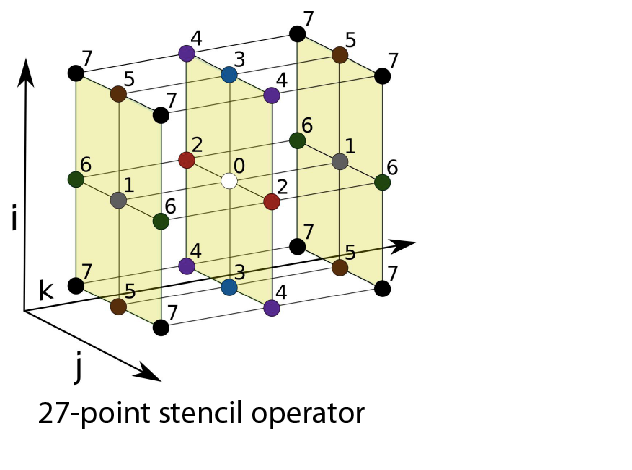
The HPCG benchmark solves the Poisson equation on a three-dimensional domain. A discretization on a global grid with a 27-point stencil at each grid point generates a system of linear equations with a large, sparse, highly structured system matrix. This system is solved by a preconditioned conjugate gradient method. The unknowns in this system are distributed to a 3-D grid of parallel MPI processes.
 |
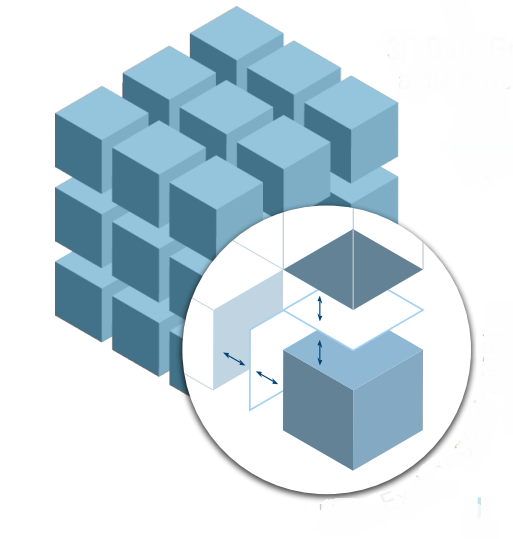 |
| 27-point stencil | 3-D process grid. |
A problem with a sparse system matrix and an iterative solution technique is more relevant to many applications than the dense system matrix of the LINPACK benchmark.
Experimental Design
The HPCG benchmark uses a 3-D grid of P = px x py x pz parallel MPI processes. We consider P = 1, 8, 64, 512 in our experiments. Each process hosts a local subgrid of size nx x ny x nz. Thus, Nx = nx px, Ny = ny py, and Nz = nz pz, and the total number of unknowns Nx x Ny xNz scales with the number of processes.
For example for P = 512 processes, the global grid ranges from millions to billions of unknowns:
| n | P = 1 | P = 8 | P = 64 | P = 512 |
|---|---|---|---|---|
| 16 | 4,096 | 32,768 | 262,144 | 2,097,152 |
| 32 | 32,768 | 262,144 | 2,097,152 | 16,777,216 |
| 64 | 262,144 | 2,097,152 | 16,777,216 | 134,217,728 |
| 128 | 2,097,152 | 16,777,216 | 134,217,728 | 1,073,741,824 |
| 256 | 16,777,216 | 134,217,728 | 1,073,741,824 | 8,589,934,592 |
Results
We ran the HPCG Benchmark Revision 2.4 with execution time 60 seconds using the Intel C++ compiler and MVAPICH2. The table shows the observed GFLOP/s for several local subgrid dimensions nx x ny x nz. The table reports the results for P = 512 parallel MPI processes using Ncompute nodes withpN processes per node and nt OpenMP threads per MPI process. Possible combinations for P = 512 are N = 32 nodes withpN = 16 processes per node and nt = 1 thread per process or N = 64 nodes with pN = 8 processes per node and nt = 1 or 2 threads per process.
| nx = ny = nz = 16 | nt = 1 | nt = 2 | |
|---|---|---|---|
| N = 32 pN = 16 | 45.58 | N/A | |
| N = 64 pN = 8 | 113.50 | 112.36 | |
| nx = ny = nz = 32 | nt = 1 | nt = 2 | |
| N = 32 pN = 16 | 170.03 | N/A | |
| N = 64 pN = 8 | 209.92 | 211.84 | |
| nx = ny = nz = 32 | nt = 1 | nt = 2 | |
| N = 32 pN = 16 | 223.92 | N/A | |
| N = 64 pN = 8 | 209.62 | 238.82 | |
| nx = ny = nz = 128 | nt = 1 | nt = 2 | |
| N = 32 pN = 16 | 233.98 | N/A | |
| N = 64 pN = 8 | 210.94 | 230.42 |
The table allows us to conclude:
- Larger problems allow for better performance, as calculation time dominates communication time.
- Increasing the number of threads per MPI process may increase computational throughput as delays in memory access are masked by process switching.
- Optimal performance is achieved using all 16 cores per node, whether via MPI processes or via OpenMP multi-threading.
Links
Sandia HPCG Benchmark: http://software.sandia.gov/hpcg/
Adam Cunningham, Gerald Payton, Jack Slettebak, Jordi Wolfson-Pou, Jonathan Graf, Xuan Huang, Samuel Khuvis, Matthias K. Gobbert, Thomas Salter, and David J. Mountain. Pushing the Limits of the Maya Cluster. Technical Report HPCF-2014-14, UMBC High Performance Computing Facility, University of Maryland, Baltimore County, 2014. Reprint in HPCF publications list
Poster presented at the Summer Undergraduate Research Fest (SURF)
Click here to view Team 1’s project
Click here to view Team 2’s project
Click here to view Team 3’s project
Click here to view Team 5’s project