| Team Members: | Nancy Hong1, Emily Jasien2, Christopher Pagan3, and Daniel Xie4 |
| Graduate Research Assistant: | Zana Coulibaly5 |
| Faculty Mentor: | Kofi P. Adragni5 |
| Client: | Ian F. Thorpe6 |
1Department of Mathematics, Stony Brook University,
2Department of Mathematics, California State Polytechnic University, Pomona,
3Department of Computer Science and Electrical Engineering, University of Maryland, Baltimore County,
4Division of Natural Sciences, New College of Florida,
5Department of Mathematics and Statistics, University of Maryland, Baltimore County,
6Department of Chemistry and Biochemistry, University of Maryland, Baltimore County

Team 1, from left to right: Nancy Hong, Kofi P. Adragni, Christopher Pagan, Emily Jasien, Daniel Xie, Zana Coulibaly.
About the Team
Our team consisted of Nancy Hong, Emily Jasien, Christopher Pagan, and Daniel Xie. We worked on a problem involving the detection of nonlinear relationships among spatial variables, with applications to protein motion in mind. Our work was conduced in summer 2014 at the UMBC REU Site: Interdisciplinary Program in High Performance Computing, under the supervision of Dr. Kofi P. Adragni from the UMBC Department of Mathematics and Statistics as well as graduate assistant Zana Coulibaly. Our problem was originally posed by Dr. Ian F. Thorpe from the Department of Chemistry and Biochemistry at UMBC.
Problem Posed
Allostery is a process in which an event that occurs at one region in a complex macromolecule can create a change at a distant, coupled region in that molecule. We look at this process in proteins and the motional correlations that result.
A commonly used measure of correlation, Pearson’s correlation coefficient, is suitable only for measuring linear trends. When dealing with spatial information, however, we desire a measure of correlation that can detect non-linear relationships as well.
How can we find an accurate method to determine both linear and non-linear motional correlations in proteins?
Methodology and Implementation
We devise a solution by using polynomial regressions of various degrees to check for relationships. This reasoning behind this comes from the ability of polynomials to approximate a large class of functional forms, allowing us to detect a wide variety of relationships.
To determine the optimal degree of polynomial to use for the model, k-fold cross-validation is used. The data set is divided into k bins, with one bin used to test the model created from the other k-1 bins by calculating the mean squared prediction error.
The model with the smallest mean squared prediction error is chosen. We then estimate the strength of relationships between the variables by using the R value associated to the regression, which is our alternative to the Pearson correlation coefficient. Our final results are stored in a correlation matrix containing comparisons for all the variables of interest.
We implemented the methodology by using the statistical programming language R. The code calculates the optimal degree of the linear models and produces a matrix of correlations between all random variables. The code was also made for parallel processing using the cluster maya at the High Performance Computing Facility (HPCF). The libraries used are ‘MPV’, ‘Rmpi’, and ‘snow’.
In order to test our method, we simulated data of various functions that are correlated to see if our methodology produces correct and relatively consistent results. Sample noise data was also simulated to test whether or not the code will find correlations where there should not be. The code generated heatmaps to visually inspect the relationships picked up in simulated data.
Results and Conclusions
Heatmap of the correlation matrix generated by our method versus correlation matrix created from the absolute value of Pearson correlation coefficients:
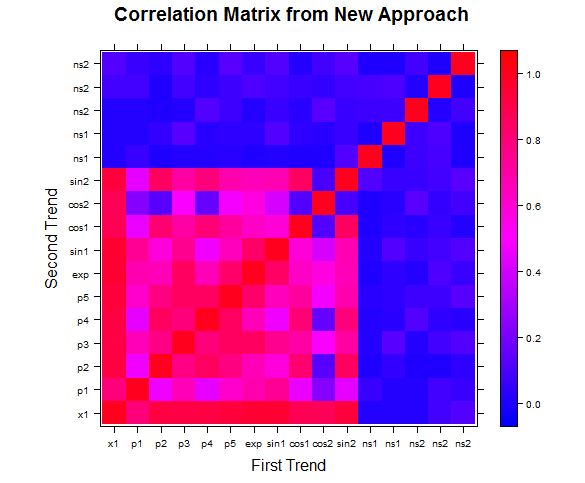 |
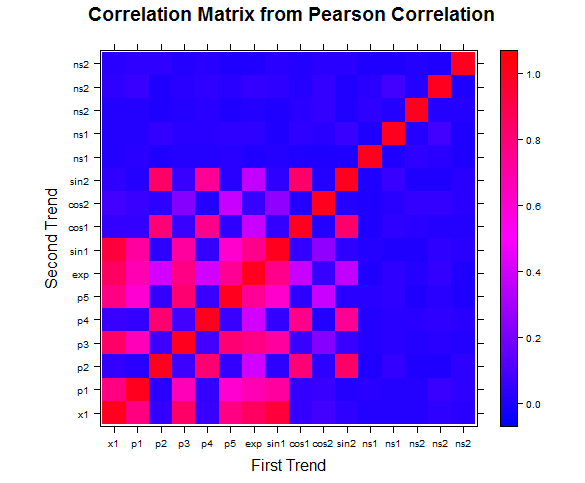 |
| 1a | 1b |
Figure 1: Our measure of correlation picks up many more relationships without significantly picking up noise in the process.
Future Work
There are many possible extensions of this project that can be conducted using our work. A natural one would be to test the performance of this measure of correlation against that of other alternate measures of correlation, such as distance correlation or ones based on mutual information. It would be enlightening to assess their relative strengths and weakness at detecting trends on a large and diverse simulated data set.
Links
Nancy Hong, Emily Jasien, Christopher Pagan, Daniel Xie, Zana Coulibaly, Kofi P. Adragni, and Ian F. Thorpe. Nonlinear Measurers of Correlation and Dimensionality Reduction with Application to Protein Motion. Technical Report HPCF-2014-11, UMBC High Performance Computing Facility, University of Maryland, Baltimore County, 2014. (HPCF machines used: maya.). Reprint in HPCF publications list
Poster presented at the Summer Undergraduate Research Fest (SURF)
Click here to view Team 2’s project
Click here to view Team 3’s project
Click here to view Team 4’s project
Click here to view Team 5’s project