| Team Members: | Fernando X. Avila-Soto1, Alec N. Beri2, Eric Valenzuela3, and Abenezer Wudenhe4 |
| Graduate Assistants: | Ari Rapkin Blenkhorn4, Jonathan S. Graf5, and Samuel Khuvis5 |
| Faculty Mentor: | Matthias K. Gobbert5 |
| Clients: | Jerimy Polf6 |
1Department of Computer Science and Mathematics, Muskingum University,
2Department of Computer Science, University of Maryland, College Park,
3Department of Computer Science, California State University, Channel Islands,
4Department of Computer Science and Electrical Engineering, University of Maryland, Baltimore County
5Department of Mathematics and Statistics, University of Maryland, Baltimore County,
6Department of Radiation Oncology, University of Maryland – School of Medicine
About the Team
Our team, which consisted of Fernando Avila-Soto, Alec Beri, Eric Valenzuela, and Abenezer Wudenhe, participated in the Interdisciplinary Program in High Performance Computing located in the Department of Mathematics and Statistics at UMBC. Our project consisted of applying parallel computing techniques to the Stochastic Origin Ensemble (SOE) algorithm for the reconstruction of images of secondary gammas emit-ted during proton beam therapy. We use OpenMP and CUDA to optimize the C++ implementation of the algorithm on CPUs and a hybrid CPU/GPU approach. Assisting us in our research and providing insight and supervision was our faculty mentor, Dr. Matthias K. Gobbert, along with our graduate research assistants, Ari Rapkin Blenkhorn, Jonathan Graf, and Samuel Khuvis.
Application
Radiation therapy is a common technique used in medicine to treat cancerous tumors. It uses high energy X-rays to damage the DNA of cancer cells and stop the cells from reproducing. It is important to note that radiation also damages normal cells. For our research purposes, we are interested in external radiation therapy, in which the radiation beam is administered from outside the body. Conventional forms of radiation treatment may include using X-ray beams. The cross-section of a patient’s chest in the figure demonstrates a comparison between X-ray beams and proton beams. X-ray beams have the potential to penetrate through the entire body, damaging critical organs such as the heart highlighted in orange/red. By contrast, a proton beam allows doctors better control over irradiation of cancerous tissue, since they can control the depth of the proton beam.
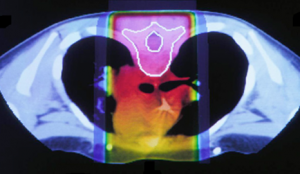
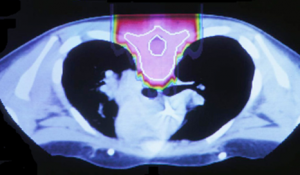
In order to fully exploit the advantages of proton radiation therapy, there is a need for a method of verifying the (in-vivo) beam range. In particular, the beam range verification must be fast and precise so that doctors can control the beam in real time. For this particular problem, image reconstruction is done with a stochastic origin ensemble algorithm (SOE).
UMBC High Performance Computing Facility
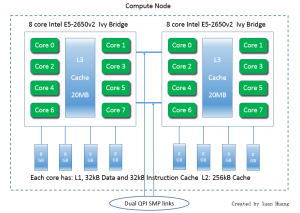
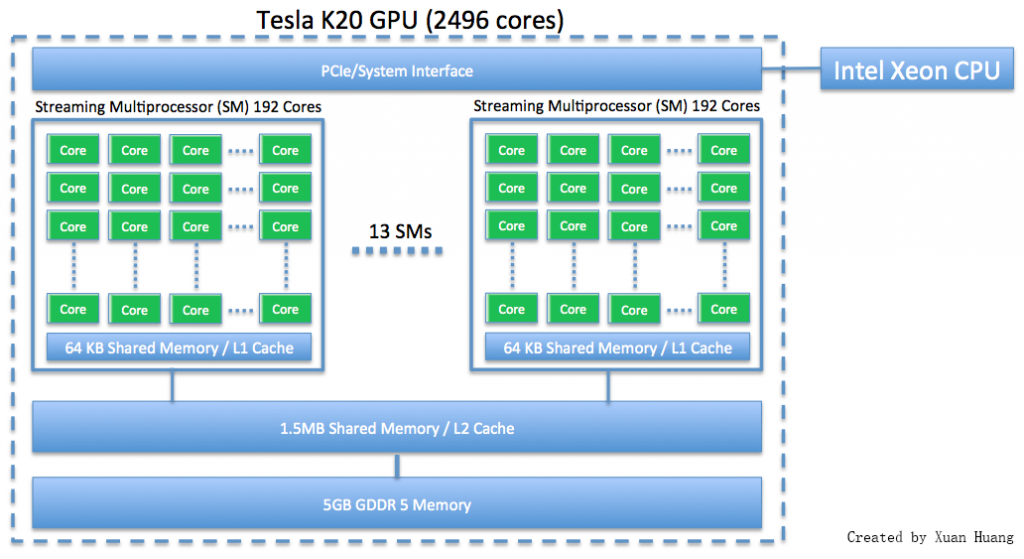
The 240-node cluster maya contains 72 nodes with two eight-core 2.6 GHz Intel E5-2650v2 Ivy Bridge CPUs and 64 GB memory. These nodes include 19 hybrid nodes that contain two NVIDIA Tesla K20 GPUs each. Each GPU is equipped with 2496 cores and 5 GB of memory.
The figure shows a schematic of a compute node with two eight-core CPUs, showing that a total of 16 computational cores are available in one compute node. The schematic of the Tesla K20 GPU in the figure shows the arrangements of the total number of 2496 cores in 13 streaming multiprocessors (SM), each with 192 cores.
Utilizing the GPUs on the cluster, the CUDA API and runtime environment, we parallelized the portion of the SOE algorithm that performs density estimation and likely origin selection. The 2496 cores on the Tesla K20 GPU allow us to run a massive number of threads concurrently. When a function is called from the CPU to be run on the GPU, the threads on which the function runs are grouped into a grid of thread blocks. Each thread block contains the same number of threads as every other thread block, and each thread block can allocate memory that is shared among all of its threads. In addition, all the threads in a block can be synchronized (all threads will stop at a specific point in the code and wait until all other threads have reached the same point). The number of blocks and threads per block are parameters specified by the user in the function call.
Performance Results
For the performance comparisons between multi-threaded CPU code and our new hybrid CPU/GPU implementation, we use two test cases. One has a small input file with approximately 15,000 detected gammas and one with a large input file with approximately 380,000 gammas. The performance studies use 1,000 iterations and standard definition (SD) with voxels of about 40 cubic millimeters volume.
The first table shows the run time of the SOE algorithm on the CPU and compares the speedup time small and large file sizes. Using 1 thread as the control and comparing other runs, we see speedup as we increase the number of threads up to 16 threads. When we hit 32 threads, there is a decrease in efficiency. This is expected for multi-core CPUs, whose cores are most efficient at processing only one thread.
Performance study on a single node with two eight-core CPUs.
(a) Wall clock time in seconds
| 1 thread | 2 threads | 4 threads | 8 threads | 16 threads | 32 threads | |
| Small | 40 | 22 | 13 | 8 | 6 | 6 |
| Large | 955 | 513 | 286 | 163 | 101 | 108 |
(b) Observed speedup
| 1 thread | 2 threads | 4 threads | 8 threads | 16 threads | 32 threads | |
| Small | 1 | 1.82 | 3.08 | 5.00 | 6.67 | 6.67 |
| Large | 1.00 | 1.86 | 3.34 | 5.86 | 9.45 | 8.84 |
For our hybrid CPU/GPU runs in the second table we start with a base case of 512 threads. We then increase the number of threads by factors of 2, up to two cases with more threads than total number of 2496 cores available on the GPU, allowing us to conclude whether or not hyperthreading can be effective on the GPU. The definition of speedup on the GPU as modified to take the 512 thread case as base case.
The table of hybrid CPU/GPU runs shows that run times decrease with increasing numbers of threads. This decrease continues all the way to the largest number of 8192 threads in the table, which confirms that hyperthreading is effective on the GPU.
Comparing both tables, we see in the first column that the GPU runs are slower than the CPU runs. This is not indicative of any problem, since the choice of 512 threads is artifical on a GPU with many more cores available. Rather, on a massively parallel device such as a GPU, it is natural to use as many threads as possible at all times, as confirmed to be effective above for 8192 threads. Therefore, using the CPU implementation with 1 thread as the comparison, we see a speedup of the 8192 threads GPU run over the serial CPU run of about 4x.
Performance study on one GPU of a hybrid CPU/GPU node.
(a) Wall clock time in seconds
| 512 threads | 1024 threads | 2048 threads | 4096 threads | 8192 threads | |
| Small | 93 | 60 | 38 | 25 | 15 |
| Large | 2061 | 1245 | 660 | 382 | 229 |
(b) Observed speedup
| 512 threads | 1024 threads | 2048 threads | 4096 threads | 8192 threads | |
| Small | 1 | 1.55 | 2.45 | 3.72 | 6.20 |
| Large | 1.00 | 1.66 | 3.13 | 5.40 | 9.00 |
Using strictly powers of 2 did not allow us to use the maximum number of threads that can be run on the GPU. Using CUDA’s maximum number of 1024 threads per block and 13 thread blocks, consistent with the GPU having 13 streaming multiprocessors (SM),
for a total of 13,312 threads, the fastest run time we achieved on a CPU/GPU run with the large file size (380,000 detected gammas) was 196 seconds. Compared to the serial CPU run time of 955 seconds, this is about a 5x speedup.
Conclusions and Future Work
By making use of the CUDA API and runtime environment, we were able to successfully port the code given to us to a hybrid CPU/GPU architecture. We were able to achieve a maximum speedup (when comparing to the serial CPU run) of about 5x by using a total of 13,312 threads on the GPU. This demonstrates that increasing the number of threads past the number of total of physical cores (2496) still results in a substantial speedup, unlike the behavior that occurs on a compute node when the number of threads is greater than the number of available cores.
Our hybrid implementation is not optimal. This code may be able to be optimized further to the point where it can be run on the cluster maya with better performance than an OpenMP run with 16 threads on a single node.
Links
Fernando X. Avila-Soto, Alec N. Beri, Eric Valenzuela, Abenezer Wudenhe, Ari Rapkin Blenkhorn, Jonathan S. Graf, Samuel Khuvis, Matthias K. Gobbert, and Jerimy Polf. Parallelization for fast image reconstruction using the stochastic origin ensemble method for proton beam therapy. Technical Report HPCF-2015-27, UMBC High Performance Computing Facility, University of Maryland, Baltimore County, 2015. (HPCF machines used: maya.). Reprint in HPCF publications list
Poster presented at the Summer Undergraduate Research Fest (SURF)
Click here to view Team 1’s project
Click here to view Team 2’s project
Click here to view Team 3’s project
Click here to view Team 4’s project
Click here to view Team 5’s project
Click here to view Team 6’s project
Click here to view Team 8’s project
