| Team Members: | Sergio Garcia Tapia1, Rebecca Hsu2, Alyssa Hu3, and Darren Stevens II4 |
| Graduate Assistant: | Jonathan S. Graf5 |
| Faculty Mentor: | Matthias K. Gobbert5 |
| Client: | Tyler Simon6 |
1Department of Mathematics, University at Buffalo, SUNY,
2Department of Mathematics, University of Maryland, College Park,
3Departments of Mathematics and of Computer Science, University of Maryland, College Park,
4Department of Computer Science and Electrical Engineering, University of Maryland, Baltimore County
5Department of Mathematics and Statistics, University of Maryland, Baltimore County,
6Laboratory for Physical Sciences
Motivation
Many application problems in data analysis inherently contain multidimensional data, also known as tensors. Oftentimes, summaries about the data are desired for a study, for which methods such as principal component analysis are useful. For N-dimensional tensors, an alternative approach is to compute and interpret tensor decompositions of the original multidimensional data.
Tensor Basics
A tensor is an N-way array used to store data, and is thus a generalization of a matrix. A Tucker decomposition, also known as 3 Mode PCA (3MPCA), can be used to express a 3-way tensor X with real entries of size I-by-J-by-K as a tensor product of a core tensor and three component matrices. The core tensor G is of size P-by-Q-by-R and the three components matrices A, B, and C are of sizes I-by-P, J-by-Q, and K-by-R, respectively. The user requested integer dimensions P, Q, and R are user requested and at most I, J and K, respectively.
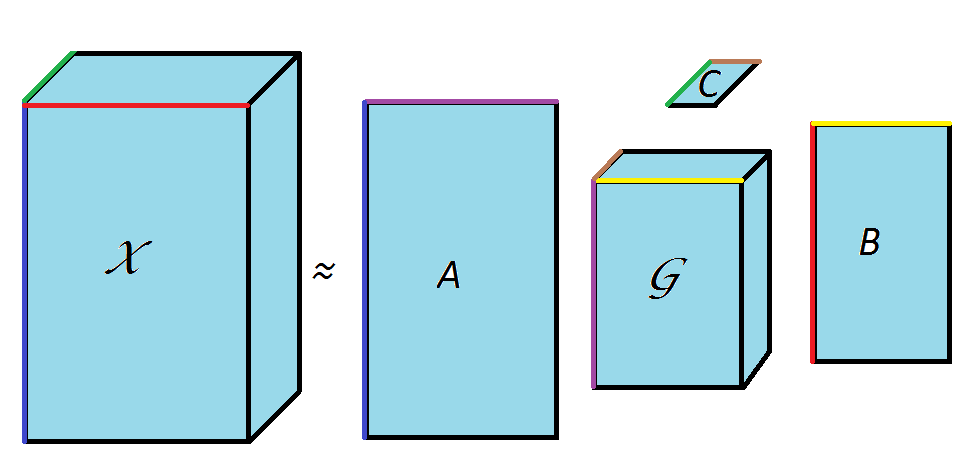
Tucker Decomposition Results for an Example
In a psychological experiment, I = 326 children were observed to display J = 5 behaviors, which are Proximity Seeking (PS), Contact Maintaining (CM), Resistance (R), Avoidance (AV), and Distance Interaction (DI), in K = 2 situations. The strength of each behavior is scored from 1 to 7, resulting in data, for instance, for the first five
children in situation 1:
Child PS CM R AV DI
1 3 2 1 2 7
2 6 7 1 1 1
3 1 2 1 2 7
4 7 7 7 1 1
5 6 4 4 1 1
The tensor describing this problem is therefore of size 326-by-5-by-2. We compute the Tucker decomposition with the tucker_als function from the Matlab Tensor Toolbox requesting a 2-by-2-by-2 core tensor. The resulting matrices are a 2-by-2-by-2 core matrix G, a 326-by-2 matrix A, a 5-by-2 matrix B, and a 2-by-2 matrix C. For instance, the B matrix is then
0.5444 -0.3705
0.4363 -0.5090
0.3391 -0.1313
0.3919 0.3124
0.4947 0.6992
Interpreting Tucker results
The vectors of B are principal components. The projection of the first five children’s data onto the second column of B is
3.2583
-4.0955
3.9993
-6.0638
-3.7725
The significance of the resulting vector is that negative values correspond to the extent to which behaviors of PS and/or CM are present, whereas positive values correspond to the extent to which behaviors of AV and/or DI are present. Thus, the projections summarize information about the behavior of each child in situation 1.
Links
Sergio Garcia Tapia, Rebecca Hsu, Alyssa Hu, Darren Stevens II, Jonathan S. Graf, Matthias K. Gobbert, and Tyler Simon. Applications of Tensor Decomposition. Technical Report HPCF-2016-17, UMBC High Performance Computing Facility, University of Maryland, Baltimore County, 2016. (HPCF machines used: maya.). Reprint in HPCF publications list
Poster presented at the Summer Undergraduate Research Fest (SURF)
Click here to view Team 1’s project
Click here to view Team 2’s project
Click here to view Team 3’s project
Click here to view Team 4’s project
Click here to view Team 5’s project
Click here to view Team 6’s project

