| Team Members: | Jessica Cooley1, Aaron George 2, Zachary Mekus3, and Victoria Sabo 4 |
| Graduate Assistant: | Morgan Strezgowski1 |
| Faculty Mentor: | Brad Peercy1 |
| Client: | Michelle Starz-Gaiano5 |
1 Department of Mathematics and Statistics, University of Maryland, Baltimore County,
2 Department of Mathematics and Department of Computer Science,University of Maryland, College Park
3 Department of Computer Science and Engineering,Washington University in St. Louis
4 Department of Mathematics and Statistics,Georgetown University
5 Department of Biological Sciences,University of Maryland, Baltimore County,
About the Team
Our team, Jessica Cooley, Aaron George, Zachary Mekus, and Victoria Sabo, worked on improving a computational model of the cell cluster migration in fruit flies to help our client, Dr. Michelle Starz-Gaiano of the Department of Biological Sciences at UMBC. We were aided by our faculty mentor, Dr. Bradford Peercy, and our graduate assistant, Morgan Strzegowski.
Problem
Cell migration is an integral part of many processes such as human healing. To understand this process, experimentalists use Drosophila melanogaster, the common fruit fly, as a model system to observe cell cluster migration. We were given a computational model that simulates the six hour migration of the border and polar cell cluster in the egg chamber of Drosophila[1]. We improved the model to give a more accurate representation of the entire process of cell cluster migration, including the diffusion of chemoattractant.
Methodology
The previous model simulates the egg chamber using Identical Math Cells (IMCs), with each part of the chamber being composed of one or more IMCs. In our new model, we simulated the diffusion of the chemoattractant that causes migration and used the resulting gradient to improve the accuracy of the migration model. To model the domain of the diffusion, we imported the IMCs from the previous model and generated the space between the IMCs on the exterior of the egg chamber (the border, polar, and epithelial cells, as well as the oocyte) and the IMCs of the nurse cells. Using this geometry, we calculated the distribution of chemoattractant as it diffused across the cell. We then used the normalized gradient at each border cell to calculate the migratory force in the revised migration code.
Results
We experimented with various parameters to identify their effects on both the time required for the chemoattractant to reach the apical end of the egg chamber and the average concentration found in the egg chamber. We also tested the time needed for the concentration of chemoattractants to reach a steady state and the difference in the x components of the gradient at different points in the egg chamber. In doing so, we identified the possible ranges of each variable based on which values fit the concrete information we knew about the cell cluster migration in fruit flies.
The left figure shows the concentration of the chemoattractant on the surface of the egg chamber when its source is a portion of the epithelium and the surface of the oocyte. The right image shows the extracellular concentration of the egg chamber. The white areas portray that diffusion does not take place inside of the nurse cells. The source of the chemoattractants in the figure on the right is just the oocyte, but the concentration quantity has been adjusted such that the average concentration in the egg chamber is the same as the left diagram.Therefore, both of these figures are examples of realistic chemoattractant diffusions.
We also modified the source of chemoattractant and identified its effect on the migration of the cell cluster, specifically the time and completion rate of migration and variability of ending locations. We found that secreting from the epithelium as well as the oocyte reduces the speed and proportion of successful migrations and decreases the variability of the final locations.
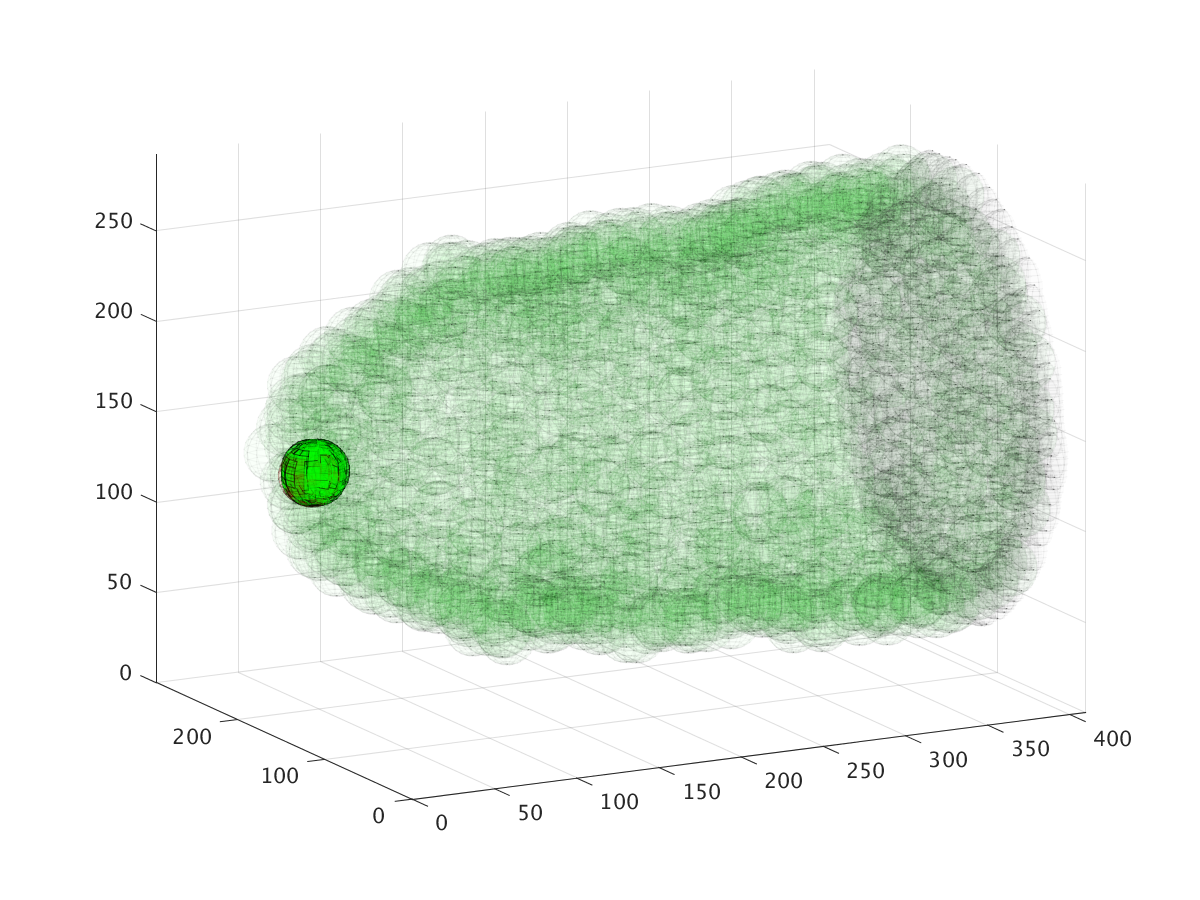
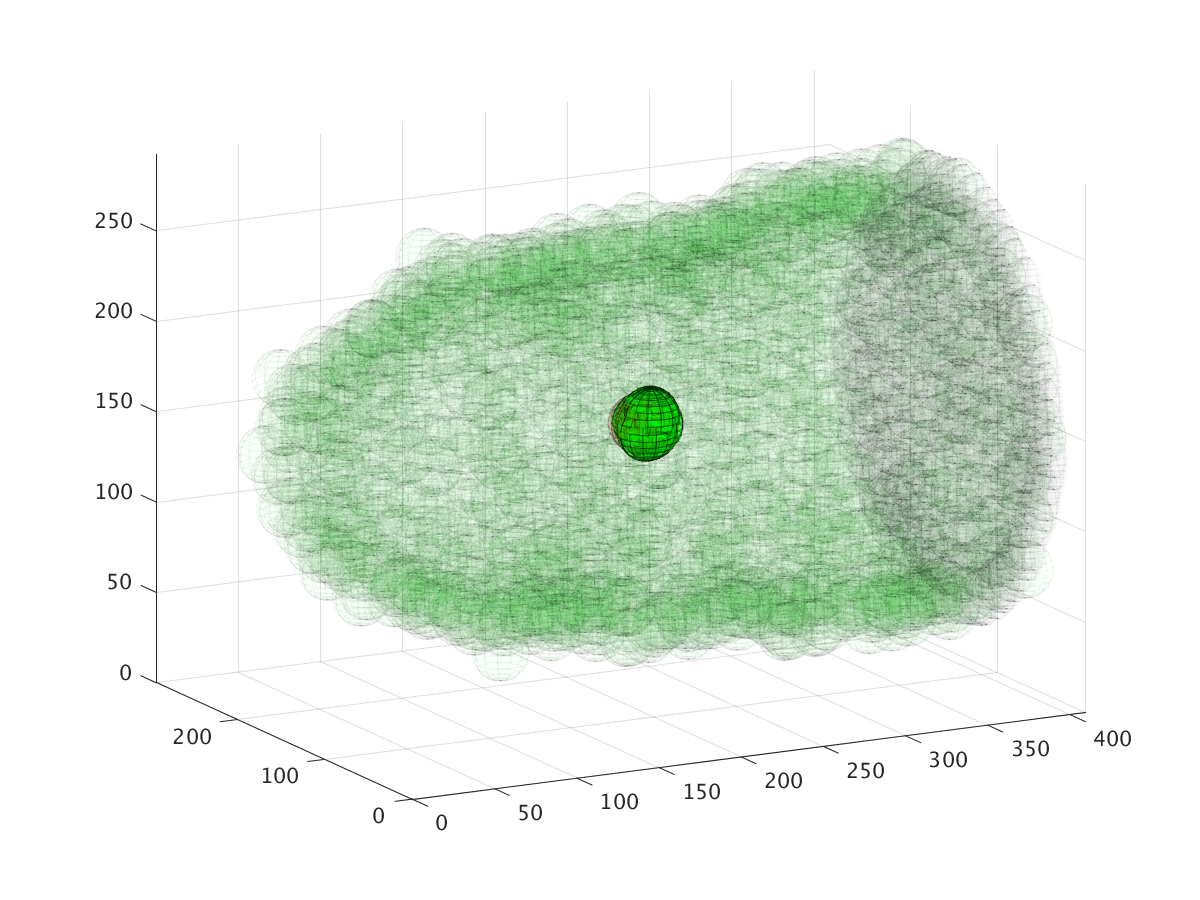
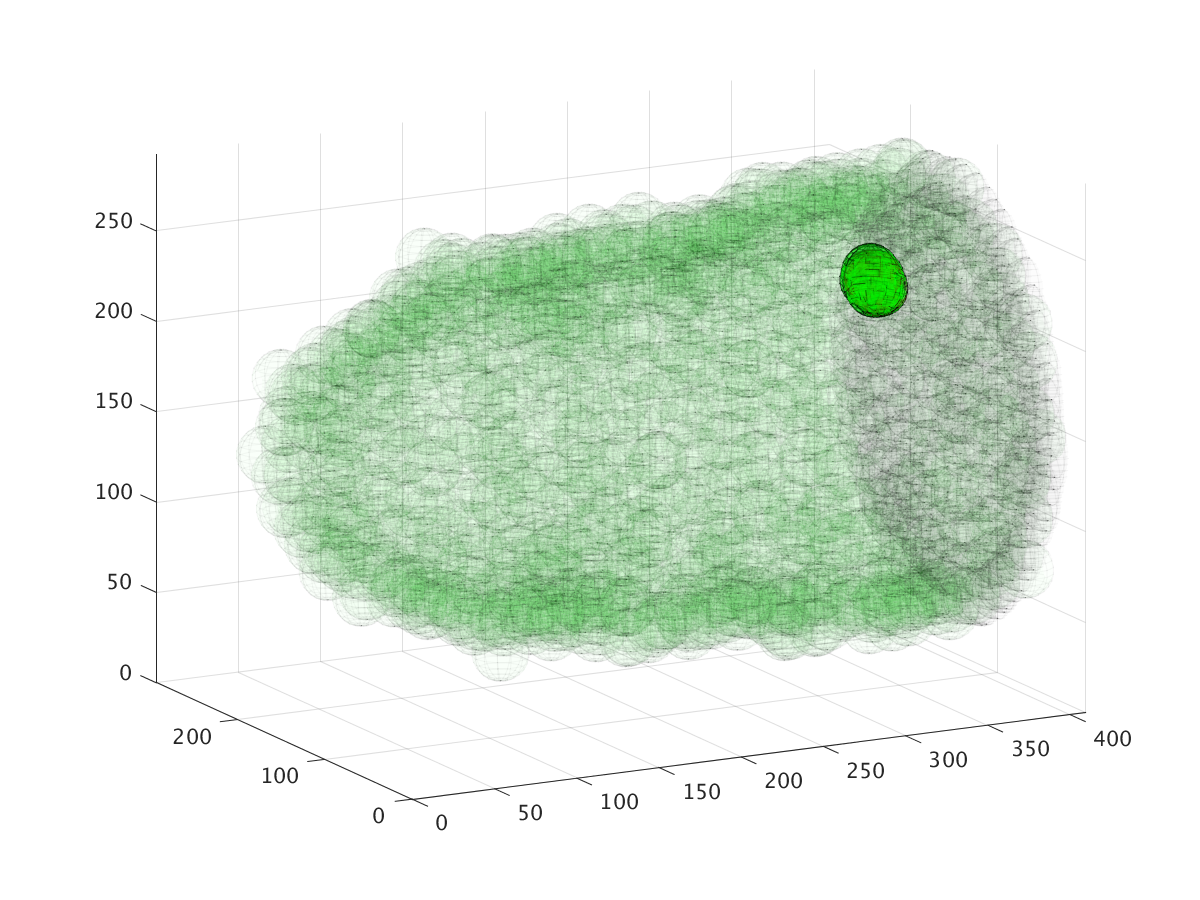
The three images above show the cluster’s location during a six hour migration, specifically at times 22.5 minutes, 3 hours, and 6 hours. Cell cluster migration uses repulsive, adhesive, migratory, and stochastic forces to simulate the migration process.
In addition, we significantly improved the speed of the model by parallelizing the code, which allowed us to remove a previous optimization where the code only checked interactions between a pre-calculated list of neighbors, improving its accuracy.
Conclusions and Future Directions
After changing the migratory interactions, we concluded that the force coefficient parameters needed to be updated to maintain realistic migration timing. We also concluded that secreting chemoattractant from the epithelium causes off-center and less consistent cluster migration. In addition, after five hours, the magnitude of the gradient at the oocyte is much greater than that at the apical end, so it likely does not linearly affect the migratory force.
For future research into this project, we would encourage further investigations into what causes the dorsal migration of the cell cluster. Also, pending a successful 3D print of an egg chamber, code can be written using that more realistic model as the domain.
Links
Jessica Cooley, Aaron George, Zachary Mekus, Victoria Sabo, Morgan Strzegowski, and Bradford Peercy. Distribution of Chemoattractants in a Heterogeneous Tissue and its Impact on Cell Cluster Migration. Technical Report HPCF-2017-13, UMBC High Performance Computing Facility, University of Maryland, Baltimore County, 2017. Reprint in HPCF publications list
[1] David P. Stonko, Lathiena Manning, Michelle Starz-Gaiano, and Bradford E. Peercy. A mathematical model of collective cell migration in a three-dimensional, heterogeneous environment. PLoS One, 10(4), 2015.
Poster presented at the Summer Undergraduate Research Fest (SURF)
Click here to view Team 1’s project
Click here to view Team 2’s project
Click here to view Team 4’s project
Click here to view Team 5’s project
Click here to view Team 6’s project