| Team Members: | Samantha Allen1, Dorothy Kirlew2, Neil Obetz3, and Derek Wade4 |
| Graduate Assistant: | April Albertine5 |
| Faculty Mentor: | Nagaraj K. Neerchal5 |
| Client: | Martin Klein6 |
1High Point University, High Point, NC
2Hood College, Frederick, MD
3Millersville University, Millersville, PA
4Boise State University, Boise, ID
5University of Maryland, Baltimore County, Baltimore, MD
6U.S. Census Bureau, Suitland, MD

Team 1, from left to right: Derek Wade, Dorothy Kirlew, Samantha Allen, Neil Obetz
About the Team
The REU Site: Interdisciplinary Program in High Performance Computing located in the Department of Mathematics and Statistics at UMBC. Our team, Samantha Allen, Dorothy Kirlew, Neil Obetz, and Derek Wade, researched population ranking methods and applied them to U.S. Census data, a project proposed by Dr. Martin Klein of the U.S. Census Bureau. The project provided us with the opportunity to utilize Bayesian and Simple Regression techniques to expand on existing ranking procedures. Supervising our work and providing much appreciated assistance were faculty advisor Dr. Nagaraj K. Neerchal and graduate assistant April Albertine, both of UMBC. Dr. Klein also added invaluable insights for our project direction as well.
Project Introduction
The U.S. Census Bureau (USCB) assists the federal government in distributing over $400 billion of aid by ranking the states according to certain criteria, such as average poverty level. The current ranking algorithm is based on sample estimates which are associated with a certain amount of error. Dr. Klein of the USCB has compared the performance of non-informative Bayesian techniques to the USCB’s current method. We expand on this work to add informed Bayesian and regression models to the comparison. By employing moderation techniques, we obtain excellent probabilities of correct rankings.
Simulation Testing
We use two of our own informed methods: Fully Informed Prior (FIP) and Regression Informed Prior (RIP) in comparison with the U.S. Census Bureau’s current method, the SI method, in the partial simulation study below. The full study and more detail is available in the technical report. The Bureau’s current method ranks the populations, Θ, by sorting the estimates and applying a corresponding rank to the sorted list. We rank the current populations with our new methods by using previous data, Θprev, to inform our ranking procedure and come up with more accurate rankings. These informed methods obtain comparable results until the current data and the previous data have dissimilar orderings, as shown in the table below. With small shifts in the previous data, FIP does slightly better, but when shifts are dramatic, RIP produces much better probabilities of a correct ranking and consistently outperforms the current method. A multiplier on the standard deviation of the previous data, τ, moderates the influence of the previous year’s data on the rankings. In the table, si is the estimated ranking and P is the probability that the population is ranked correctly.
| True | Current | Using FIP | Using RIP | |||||||
| Rank | Method | τ x 1 | τ x 2 | τ x 1 | τ x 2 | |||||
| si | P | si | P | si | P | si | P | si | P | |
| r1 | 1 | 0.93 | 1 | 0.56 | 1 | 0.88 | 1 | 0.99 | 1 | 0.92 |
| r2 | 2 | 0.56 | 3 | 0.23 | 2 | 0.51 | 2 | 0.84 | 2 | 0.58 |
| r3 | 3 | 0.43 | 2 | 0.22 | 3 | 0.39 | 3 | 0.79 | 3 | 0.48 |
| r4 | 4 | 0.56 | 5 | 0.42 | 4 | 0.50 | 4 | 0.79 | 4 | 0.63 |
| r5 | 5 | 0.63 | 4 | 0.39 | 5 | 0.57 | 5 | 0.79 | 5 | 0.70 |
The simulation settings used in this case are as follows:
Θ = 10.0, 10.5, 10.7, 11.0, 11.2 ; σ = 0.1, 0.3, 0.3, 0.1, 0.5
Θprev = 10.7, 10.5, 10.3, 10.1, 9.9 ; τ = 0.1, 0.3, 0.3, 0.1, 0.5
- The current method produces the correct ranking, si, but has relatively low probabilities of being correct.
- The ranking method utilizing the Fully Informed Prior (FIP) does not get the correct ranking with a τ multiplier of 1, but does with a multiplier of 2. However, the probabilites are still very low.
- The method using the Regression Informed Prior (RIP) gets the correct ranking right away and produces extremely high probabilities of being correct.
- We are, therefore, most confident in the ranking method that uses RIP, which produces higher probabilities of correct rankings, even when the previous data varies significantly from the current data. Utilizing this previous data allows us to specify a more realistic model for the prior distribution of the current data.
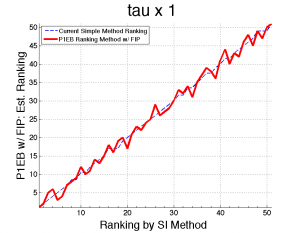
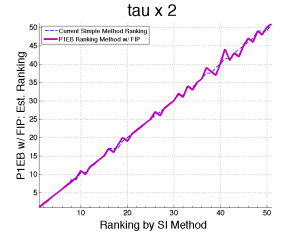
The following plots show the effect of the τ multiplier as applied to the ranked state data for 2008. Notice with the multiplier at 1, the ranking is unstable and jumps around. This is because the ranking mostly reflects the previous year’s data. When the multiplier is increased, the ranking becomes more reliable and a more accurate ranking of the current populations is established, once again reinforcing the results from the simulation study.
Applying the Bootstrap in Parallel
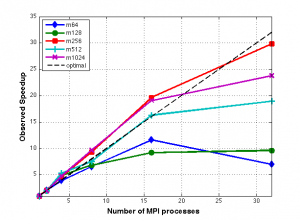
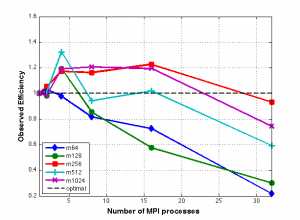
In practice, the accuracy of the estimated ranks are computed by a bootstrap. We implement this computationally expensive procedure in parallel. As the size of the bootstrap, m, increases, so does the time required to compute the estimates, and as p increases, the time required decreases. A time study is conducted and is included in the technical report. The speedup and efficiency plots for this parallel implementation, as applied to the 2008 state data, can be seen below.
Links
Samantha Allen, Dorothy Kirlew, Neil Obetz, Derek Wade, April Albertine, Nagaraj K. Neerchal, and Martin Klein. Assessment of Simple and Alternative Bayesian Ranking Methods Utilizing Parallel Computing. Technical Report HPCF-2011-11, UMBC High Performance Computing Facility, University of Maryland, Baltimore County, 2011. Reprint in HPCF publications list
Poster presented at the Summer Undergraduate Research Fest (SURF)
Click here to view Team 2’s project
Click here to view Team 3’s project
Click here to view Team 4’s project